-
1.
+10bu soruyu okuyanı 1 çözeni 2 kere gibeyim
-
2.
+11 -2
-
3.
+8devlet bahçeliye verin o çözer kesin
-
4.
+5cözmeyin dedeler! m1 m2 alayı dede
-
5.
+3beyler hiç kasmayın. ortada tek matematikçi var. adam şizofren amk.
-
6.
+2lan dıbına koyduğum soru soracan düzgün sor. sayılar farklı niye demiyosun bide muallak x,y ne demek yaa yannan x ve ye 1 den büyük desene bin sabahtan beri bütün olasılıkları yazdım. sonuç çıkmıyor.bi de övünüyor bin ben 15 dk çözdüm diye.sen 15 dk uçkurunu bile çözemezsin
-
7.
+2ben de 4 ve 61 olarak buldum ama çözüm çoktan açıklanmış. bulduğum cevabı araştırdığımda şöyle bir şey gördüm ki; mantıkçılara verilen sayı aralığına göre bir çok cevabı olabiliyormuş bu sorunun. ilgili matematik linki http://www.mathematik.uni...PUZZLES/logic_sum_product
ama güzel soru hacı. uyuyodum uyandım bununla uğraştım 2 saat.
şukuladım. -
8.
+2ıkı sayı da asal degıl. simdilik buraya kadar gelebıldım
-
9.
+12 dıbına koyiyim
-
10.
+1takan ananın amı !
-
11.
+1@1 senin ben dıbına koyim huur çocuğu iki saattir niye 2 ve 9 değil diyorum burda gib kafalı dıbını zütünü gibeyim senin dalyarak
-
12.
+1am biti oraya a,b>1 yazarsan ondalık sayıı sanıyoruz matematiğini gibtiğim
-
13.
+1first of all:Tümünü Göster
2 + 2 = 4 <= x + y <= 99 and
2 * 2 = 4 <= x * y <= 2450 = 49 * 50
b says, "i can not find these numbers."
then x * y cannot be prime, since it is the product of two numbers
greater than 1. it also cannot be the square of a prime number,
because x and y are not equal. if x * y had exactly two proper
divisors, then b would know the two numbers. this eliminates the
product of two distinct primes, and the cube of any prime.
a says, "i was sure that you could not find them."
yes, x + y cannot be the sum of two distinct primes, or the sum
of a prime and its square. this forces x + y to be one of the
following numbers:
11, 17, 23, 27, 29, 35, 37, 41, 47, 51, 53, 57, 59, 65, 67,
71, 77, 79, 83, 87, 89, 93, 95, 97
since all the remaining sums are odd, one of the two numbers must be
odd and the other even. x * y must then be even.
b says, "then, i found these numbers."
b can throw away any factorization of x * y in which the sum of the
two factors is not one of these numbers. there must be exactly one
such possibility left for him to know the numbers. this eliminates
x * y = 12, for example, because even though it has factorizations
2 * 6 and 3 * 4, the sums of the two factors, 8 and 7 respectively,
are not in the set of possible sums, so there are no possibilities
left. it also throws out x * y = 120, because 120 = 5 * 24 = 15 * 8,
and 5 + 24 = 29 and 15 + 8 = 23, which are both on the list, so there
are two possibilities left. this limits the possibilities for the
product to:
18 = 9 * 2, 9 + 2 = 11
24 = 8 * 3, 8 + 3 = 11
28 = 7 * 4, 7 + 4 = 11
50 = 25 * 2, 25 + 2 = 27
52 = 13 * 4, 13 + 4 = 17
54 = 27 * 2, 27 + 2 = 29
76 = 19 * 4, 19 + 4 = 23
92 = 23 * 4, 23 + 4 = 27
96 = 32 * 3, 32 + 3 = 35
98 = 49 * 2, 49 + 2 = 51
100 = 25 * 4, 25 + 4 = 29
112 = 16 * 7, 16 + 7 = 23
124 = 31 * 4, 31 + 4 = 35
140 = 35 * 2, 35 + 2 = 37
144 = 48 * 3, 48 + 3 = 51
148 = 37 * 4, 37 + 4 = 41
152 = 19 * 8, 19 + 8 = 27
160 = 32 * 5, 32 + 5 = 37
172 = 43 * 4, 43 + 4 = 47
176 = 16 * 11, 16 + 11 = 27
188 = 47 * 4, 47 + 4 = 51
192 67
198 29
208 29
212 57
216 35
220 59
222 77
228 79
230 51
232 37
234 35
238 41
244 65
246 47
250 35
... ...
a says, "if you could find them, then i also found them."
this means that the sum in the last preceding list must occur only
once. that eliminates x + y = 11, 27, 29, 23, 35, 51, 37, 41, 47, ... ,
leaving only a single sum that occurs only once in the above table.
this tells you x and y and how a and b figured them out. -
14.
+1@78 lan malak o zaman m2 niye bulamasın kaç tane sayının çarpımı 194
-
15.
+1@166 lan tamam dıbına koyim geçti. bi sakinleş, bi otur soluklan yeğen. 15 dakikada soru çözen adamsın lan sen. azıcık ağırdan al. koçum benim be. zeka fışkırıyo adamdan beyler. 15 dakika lan bu! boru mu dıbına koyim!
-
16.
+1@1 soruyu size çözdürüp tezini hocasına sunacak beyler
-
17.
+1lan binler çözen bi anlatsın laaaaaan
-
18.
+1m1 niye m2 ye bulamayacağını biliyordum diyor buna yorum getiremiyorum ben de.
-
19.
+1@78 düşükleri bulamıyomu amın feryadı adam hatasız düşünüyomuş
-
20.
+1@114 bence intihara sürüklen bin bizi mi gibtin
-
ccc rammstein ccc günaydın diler 03 01 2025
-
herkes buraya hayat felsefesini yazıyor
-
ferdi baba ölmüş
-
sozlukte gorevli yazar olunca
-
hornet gibi kız bulma uygulaması önerin la
-
 sevgilisini bavula koyup nefessiz bırakarak öldren
sevgilisini bavula koyup nefessiz bırakarak öldren -
yangın söndürme uçaklarını satçaklarmış
-
ne ilksin nede son olacaksın
-
boyle yasayacagima geberirim
-
şu mecraya gelip niye
-
 gwynplaine adlı yazarı ifşalııyorum
gwynplaine adlı yazarı ifşalııyorum -
sanatsal bir şiir
-
baskette habire barem degisiyo ya da kapaniuo
-
beyler sözlükteki herkes benden nefret ediyor
-
 asyali birini dövemeyen slav eziği
asyali birini dövemeyen slav eziği -
gassal denilen djziyi izleyen en fhafif tabirle
-
video tmp name yokk
-
 sozluge gelen yeni cocugun ppsine bakın
sozluge gelen yeni cocugun ppsine bakın -
inci sözlük bile yapayalnız
-
 eppek çıktı bugün
eppek çıktı bugün -
şimdi mutluyum sabah kötüydüm
-
am flm var mi la
-
kızlar benden tırsıyormu ne anlamadım
-
rahibe de değil lakin ortalık malı da olmamış
-
bilkentli kızlar dehşet bişey panpalar
-
 karabasan diye bi sey yok
karabasan diye bi sey yok -
beyler amerikada yaşayan bir arkadaşım var
-
caner taslaman hocayı izleyen varmı
-
pluie vardı en son evlenmişti
-
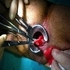 beyler bu cerrahi ameliyatın ismi ney
beyler bu cerrahi ameliyatın ismi ney - / 2