-
651.
0http://tr.wikipedia.org/wiki/Kombinasyon
Kombinasyon
Vikipedi, özgür angiblopedi
Git ve: kullan, ara
Kombinasyon, bir nesne grubu içerisinden, sıra gözetmeksizin yapılan seçimler olarak düşünülebililir, dolayısı ile nesne grubunun tekabül ettiği kümenin alt kümeleri olarak düşünebilir. Çünkü, alt kümelerde sıra önemli değildir. O halde şöyle tanımlayabiliriz: Bir A kümesinin herhangi bir alt kümesine A kümesinin bir kombinasyonu denir. Örneğin, 52 iskambil kartı arasından seçeceğiniz 4 kart, kartları seçme sıranız önemli olmadığından bir kombinasyon problemidir.
Kombinasyon özellikleri [değiştir]
• C(R, 1) = R
• C(R, R) = 1
• C(R, 0) = 1
• N = M olmak üzere C(R, N) = C(R, M) ise N + M = R
• C(R, N) = S (Sayma sayıları) ise R, N'den küçük olamaz.
Kombinasyonların sayılması [değiştir]
n elemanlı bir kümeden seçilen r elemanlı kombinasyonların toplamı (n r'den büyük veya r'ye eşit olmak üzere ) aşağıdaki formülle ifade edilir :
C(n,r)={n choose r} = {n choose {n-r}} = frac{P(n,r)}{r!} = frac{n!}{r!(n - r)!}
Kombinasyonun permütasyondan farkı, sıralamanın önemli olmamasıdır. Kombinasyonların topldıbını, P(n,r) permütasyonların topldıbını seçilen elemanların kendi aralarındaki sıralanma sayılarına (r! veya P(r,r)) bölerek bulabiliriz...
Örnek
C(5,3)={5 choose 3}={5 choose {5-3}} = frac{P(5,3)}{3!} = frac{5!}{3!(5 - 3)!}=10
C(5,3) C1 C2 C3
R1 4 3 2
R2 4 3 1
R3 4 3 0
R4 3 2 1
R5 3 2 0
R6 2 1 0 -
652.
0helal olsun adama çatır çatır ye bilader ben senın yerınde olsam gider kendıme alfa romeo guıletta alırdım bay bee
-
653.
0@1 bu gce bosum istrsn taklabilirizzzz (:
-
654.
0ruhaynz napıyosun ya liseden ben canan. canım bi ara görüşelim müsait olunca msnini ver istersen ulaşamadım bi türlü sana arayamadım, face den de bulamadım burağa falan sordum onlarda da yokmuş telefonun, pmden konuşalım canım çok özledim yaa *
-
655.
0http://tr.wikipedia.org/wiki/Kombinasyon
Kombinasyon
Vikipedi, özgür angiblopedi
Git ve: kullan, ara
Kombinasyon, bir nesne grubu içerisinden, sıra gözetmeksizin yapılan seçimler olarak düşünülebililir, dolayısı ile nesne grubunun tekabül ettiği kümenin alt kümeleri olarak düşünebilir. Çünkü, alt kümelerde sıra önemli değildir. O halde şöyle tanımlayabiliriz: Bir A kümesinin herhangi bir alt kümesine A kümesinin bir kombinasyonu denir. Örneğin, 52 iskambil kartı arasından seçeceğiniz 4 kart, kartları seçme sıranız önemli olmadığından bir kombinasyon problemidir.
Kombinasyon özellikleri [değiştir]
• C(R, 1) = R
• C(R, R) = 1
• C(R, 0) = 1
• N = M olmak üzere C(R, N) = C(R, M) ise N + M = R
• C(R, N) = S (Sayma sayıları) ise R, N'den küçük olamaz.
Kombinasyonların sayılması [değiştir]
n elemanlı bir kümeden seçilen r elemanlı kombinasyonların toplamı (n r'den büyük veya r'ye eşit olmak üzere ) aşağıdaki formülle ifade edilir :
C(n,r)={n choose r} = {n choose {n-r}} = frac{P(n,r)}{r!} = frac{n!}{r!(n - r)!}
Kombinasyonun permütasyondan farkı, sıralamanın önemli olmamasıdır. Kombinasyonların topldıbını, P(n,r) permütasyonların topldıbını seçilen elemanların kendi aralarındaki sıralanma sayılarına (r! veya P(r,r)) bölerek bulabiliriz...
Örnek
C(5,3)={5 choose 3}={5 choose {5-3}} = frac{P(5,3)}{3!} = frac{5!}{3!(5 - 3)!}=10
C(5,3) C1 C2 C3
R1 4 3 2
R2 4 3 1
R3 4 3 0
R4 3 2 1
R5 3 2 0
R6 2 1 0 -
656.
0@1 bekle lan cinsiyetimi değiştiriyorum.
-
657.
-2http://tr.wikipedia.org/wiki/Kombinasyon
Kombinasyon
Vikipedi, özgür angiblopedi
Git ve: kullan, ara
Kombinasyon, bir nesne grubu içerisinden, sıra gözetmeksizin yapılan seçimler olarak düşünülebililir, dolayısı ile nesne grubunun tekabül ettiği kümenin alt kümeleri olarak düşünebilir. Çünkü, alt kümelerde sıra önemli değildir. O halde şöyle tanımlayabiliriz: Bir A kümesinin herhangi bir alt kümesine A kümesinin bir kombinasyonu denir. Örneğin, 52 iskambil kartı arasından seçeceğiniz 4 kart, kartları seçme sıranız önemli olmadığından bir kombinasyon problemidir.
Kombinasyon özellikleri [değiştir]
• C(R, 1) = R
• C(R, R) = 1
• C(R, 0) = 1
• N = M olmak üzere C(R, N) = C(R, M) ise N + M = R
• C(R, N) = S (Sayma sayıları) ise R, N'den küçük olamaz.
Kombinasyonların sayılması [değiştir]
n elemanlı bir kümeden seçilen r elemanlı kombinasyonların toplamı (n r'den büyük veya r'ye eşit olmak üzere ) aşağıdaki formülle ifade edilir :
C(n,r)={n choose r} = {n choose {n-r}} = frac{P(n,r)}{r!} = frac{n!}{r!(n - r)!}
Kombinasyonun permütasyondan farkı, sıralamanın önemli olmamasıdır. Kombinasyonların topldıbını, P(n,r) permütasyonların topldıbını seçilen elemanların kendi aralarındaki sıralanma sayılarına (r! veya P(r,r)) bölerek bulabiliriz...
Örnek
C(5,3)={5 choose 3}={5 choose {5-3}} = frac{P(5,3)}{3!} = frac{5!}{3!(5 - 3)!}=10
C(5,3) C1 C2 C3
R1 4 3 2
R2 4 3 1
R3 4 3 0
R4 3 2 1
R5 3 2 0
R6 2 1 0 -
658.
0durun lan hesaplıyacam amk adam şow yapmış
-
659.
0@526 gerizekalı. 56 kupon var. çıkan oranı 56 ile çarpıcaksın.
-
660.
0@526 salak yemin ederim gerizekalı bu çocuk
-
661.
0adam şuan tatile gitti siz tartışın amk
-
662.
0http://tr.wikipedia.org/wiki/Kombinasyon
Kombinasyon
Vikipedi, özgür angiblopedi
Git ve: kullan, ara
Kombinasyon, bir nesne grubu içerisinden, sıra gözetmeksizin yapılan seçimler olarak düşünülebililir, dolayısı ile nesne grubunun tekabül ettiği kümenin alt kümeleri olarak düşünebilir. Çünkü, alt kümelerde sıra önemli değildir. O halde şöyle tanımlayabiliriz: Bir A kümesinin herhangi bir alt kümesine A kümesinin bir kombinasyonu denir. Örneğin, 52 iskambil kartı arasından seçeceğiniz 4 kart, kartları seçme sıranız önemli olmadığından bir kombinasyon problemidir.
Kombinasyon özellikleri [değiştir]
• C(R, 1) = R
• C(R, R) = 1
• C(R, 0) = 1
• N = M olmak üzere C(R, N) = C(R, M) ise N + M = R
• C(R, N) = S (Sayma sayıları) ise R, N'den küçük olamaz.
Kombinasyonların sayılması [değiştir]
n elemanlı bir kümeden seçilen r elemanlı kombinasyonların toplamı (n r'den büyük veya r'ye eşit olmak üzere ) aşağıdaki formülle ifade edilir :
C(n,r)={n choose r} = {n choose {n-r}} = frac{P(n,r)}{r!} = frac{n!}{r!(n - r)!}
Kombinasyonun permütasyondan farkı, sıralamanın önemli olmamasıdır. Kombinasyonların topldıbını, P(n,r) permütasyonların topldıbını seçilen elemanların kendi aralarındaki sıralanma sayılarına (r! veya P(r,r)) bölerek bulabiliriz...
Örnek
C(5,3)={5 choose 3}={5 choose {5-3}} = frac{P(5,3)}{3!} = frac{5!}{3!(5 - 3)!}=10
C(5,3) C1 C2 C3
R1 4 3 2
R2 4 3 1
R3 4 3 0
R4 3 2 1
R5 3 2 0
R6 2 1 0 -
663.
0http://tr.wikipedia.org/wiki/Kombinasyon
Kombinasyon
Vikipedi, özgür angiblopedi
Git ve: kullan, ara
Kombinasyon, bir nesne grubu içerisinden, sıra gözetmeksizin yapılan seçimler olarak düşünülebililir, dolayısı ile nesne grubunun tekabül ettiği kümenin alt kümeleri olarak düşünebilir. Çünkü, alt kümelerde sıra önemli değildir. O halde şöyle tanımlayabiliriz: Bir A kümesinin herhangi bir alt kümesine A kümesinin bir kombinasyonu denir. Örneğin, 52 iskambil kartı arasından seçeceğiniz 4 kart, kartları seçme sıranız önemli olmadığından bir kombinasyon problemidir.
Kombinasyon özellikleri [değiştir]
• C(R, 1) = R
• C(R, R) = 1
• C(R, 0) = 1
• N = M olmak üzere C(R, N) = C(R, M) ise N + M = R
• C(R, N) = S (Sayma sayıları) ise R, N'den küçük olamaz.
Kombinasyonların sayılması [değiştir]
n elemanlı bir kümeden seçilen r elemanlı kombinasyonların toplamı (n r'den büyük veya r'ye eşit olmak üzere ) aşağıdaki formülle ifade edilir :
C(n,r)={n choose r} = {n choose {n-r}} = frac{P(n,r)}{r!} = frac{n!}{r!(n - r)!}
Kombinasyonun permütasyondan farkı, sıralamanın önemli olmamasıdır. Kombinasyonların topldıbını, P(n,r) permütasyonların topldıbını seçilen elemanların kendi aralarındaki sıralanma sayılarına (r! veya P(r,r)) bölerek bulabiliriz...
Örnek
C(5,3)={5 choose 3}={5 choose {5-3}} = frac{P(5,3)}{3!} = frac{5!}{3!(5 - 3)!}=10
C(5,3) C1 C2 C3
R1 4 3 2
R2 4 3 1
R3 4 3 0
R4 3 2 1
R5 3 2 0
R6 2 1 0 -
664.
0amk werderin 1 golü sana kaç milyara patlıcak biliyonmu o 125 20-30 milyarlara düşer
-
665.
0beyler biri ozet gecsin, am var dediler geldik var mi harbiden kafam karisti
-
666.
0noldu tuttumu lan
-
667.
0http://tr.wikipedia.org/wiki/Kombinasyon
Kombinasyon
Vikipedi, özgür angiblopedi
Git ve: kullan, ara
Kombinasyon, bir nesne grubu içerisinden, sıra gözetmeksizin yapılan seçimler olarak düşünülebililir, dolayısı ile nesne grubunun tekabül ettiği kümenin alt kümeleri olarak düşünebilir. Çünkü, alt kümelerde sıra önemli değildir. O halde şöyle tanımlayabiliriz: Bir A kümesinin herhangi bir alt kümesine A kümesinin bir kombinasyonu denir. Örneğin, 52 iskambil kartı arasından seçeceğiniz 4 kart, kartları seçme sıranız önemli olmadığından bir kombinasyon problemidir.
Kombinasyon özellikleri [değiştir]
• C(R, 1) = R
• C(R, R) = 1
• C(R, 0) = 1
• N = M olmak üzere C(R, N) = C(R, M) ise N + M = R
• C(R, N) = S (Sayma sayıları) ise R, N'den küçük olamaz.
Kombinasyonların sayılması [değiştir]
n elemanlı bir kümeden seçilen r elemanlı kombinasyonların toplamı (n r'den büyük veya r'ye eşit olmak üzere ) aşağıdaki formülle ifade edilir :
C(n,r)={n choose r} = {n choose {n-r}} = frac{P(n,r)}{r!} = frac{n!}{r!(n - r)!}
Kombinasyonun permütasyondan farkı, sıralamanın önemli olmamasıdır. Kombinasyonların topldıbını, P(n,r) permütasyonların topldıbını seçilen elemanların kendi aralarındaki sıralanma sayılarına (r! veya P(r,r)) bölerek bulabiliriz...
Örnek
C(5,3)={5 choose 3}={5 choose {5-3}} = frac{P(5,3)}{3!} = frac{5!}{3!(5 - 3)!}=10
C(5,3) C1 C2 C3
R1 4 3 2
R2 4 3 1
R3 4 3 0
R4 3 2 1
R5 3 2 0
R6 2 1 0 -
668.
0resimler niye silindi lan pij
-
669.
0@1 ben senin almanya'daki dayının yavrum *
-
670.
0ibret alınıyor:loading%99...
-
ccc rammstein ccc günaydın diler 28 01 2025
-
 vikings şu acayipe çaylak at artık sol frameyi
vikings şu acayipe çaylak at artık sol frameyi -
ülkenin yarısı kürt diyorlar doğru mu
-
 mabel matiz türkiyenin en delikanlı sanatçısıdr
mabel matiz türkiyenin en delikanlı sanatçısıdr -
ekoyu tutuklasalar da sokağa çıksak
-
 dexerin korkulu rüyası gaye su akyol
dexerin korkulu rüyası gaye su akyol -
hastalıkların yüzde 90 nı müslümanlar
-
öyle boş şeylerle enerjimi harcıyorum ki
-
adam satmak itin uğursuzun önde gideni olmak
-
 beyler 12 saat çalışıyorum
beyler 12 saat çalışıyorum -
fps oyunu oyanrken midem
-
ülkedeki resmi kürt sayıı 13 milyonmuş
-
babam arabayı satacak iletişim özürlü
-
yarım saatte 1 başlık açılacaksa
-
tırrık kafayı tırlatmış kişiye denirr
-
iki gündür yataktan ilk defa kalktım
-
zalinazurt tayyibin adayı kim
-
 adamın suratı taşağa benziyor ama
adamın suratı taşağa benziyor ama -
bugun puberte gibiyim
-
sözlükte hiç karı kalmadı dimi
-
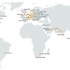 microsoft türkiyeye veri merkezi kurmamış lan
microsoft türkiyeye veri merkezi kurmamış lan -
dünyada yaşam başlamadan önce
-
üveyit baba burda servet yatıyor
-
50 şınav 23 barfix
-
 havucun taku oynayana günlülk 100 tl verseler
havucun taku oynayana günlülk 100 tl verseler -
 mabel buna çakmış mıdır
mabel buna çakmış mıdır -
 kız arkadaş yanında osbir çekmenin raconu nedir
kız arkadaş yanında osbir çekmenin raconu nedir -
 benim ne zaman sevgilim olacak ybaaaa
benim ne zaman sevgilim olacak ybaaaa -
 keşke bu bayrak altında can verebilseydim
keşke bu bayrak altında can verebilseydim -
gececi tayfa nerede lan bugün
- / 2