-
51.
022/7 ulan gerizekalılar
-
52.
012.5 falan al
-
53.
012,5 falan al
-
54.
012.5 falan al
-
55.
012.5 falan al
-
56.
031.4 falan
-
57.
012.5 falan al
-
58.
0@7 aynştayn detected.
-
59.
0Bi çemberin alanı yarıçapının karesine böl cevabı bulacaksın...
-
60.
03.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679
8214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196
4428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273
7245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094
3305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912
9833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132
0005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235
4201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859
5024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303
5982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989
3809525720106548586327886593615338182796823030195203530185296899577362259941389124972177528347913151
5574857242454150695950829533116861727855889075098381754637464939319255060400927701671139009848824012
8583616035637076601047101819429555961989467678374494482553797747268471040475346462080466842590694912
9331367702898915210475216205696602405803815019351125338243003558764024749647326391419927260426992279
6782354781636009341721641219924586315030286182974555706749838505494588586926995690927210797509302955
3211653449872027559602364806654991198818347977535663698074265425278625518184175746728909777727938000
8164706001614524919217321721477235014144197356854816136115735255213347574184946843852332390739414333
4547762416862518983569485562099219222184272550254256887671790494601653466804988627232791786085784383
8279679766814541009538837863609506800642251252051173929848960841284886269456042419652850222106611863
0674427862203919494504712371378696095636437191728746776465757396241389086583264599581339047802759009
9465764078951269468398352595709825822620522489407726719478268482601476990902640136394437455305068203
4962524517493996514314298091906592509372216964615157098583874105978859597729754989301617539284681382
686838689427741559918559252459539594310499725246808459872736446958486538
alabilirsin mesela -
61.
012,5 falandım olm ben
-
62.
012.5 Felandı
-
63.
0zorlama alabildiğin kadar
-
64.
012.5 falan al
-
65.
0o senin alışına göre değişir.
-
66.
0ben almam dokananı gibsinler, kim alırsa alsın amk...
-
67.
0pi sayısı henüz devredilen basamağı bulunamadığından sonsuza doğru gidiyor. ama kolaylık olması için 3.14 alabilirsin.
-
68.
012.5 falan al
-
69.
0(bkz: hocam spor parası için)
-
70.
0π (sometimes written pi) is a mathematical constant whose value is the ratio of any circle's circumference to its diameter in Euclidean space; this is the same value as the ratio of a circle's area to the square of its radius. It is approximately equal to 3.14159265 in the usual decimal notation. Many formulae from mathematics, science, and engineering involve π, which makes it one of the most important mathematical constants.[1]
π is an irrational number, which means that its value cannot be expressed exactly as a fraction m/n, where m and n are integers. Consequently, its decimal representation never ends or repeats. It is also a transcendental number, which implies, among other things, that no finite sequence of algebraic operations on integers (powers, roots, sums, etc.) can be equal to its value; proving this was a late achievement in mathematical history and a significant result of 19th century German mathematics. Throughout the history of mathematics, there has been much effort to determine π more accurately and to understand its nature; fascination with the number has even carried over into non-mathematical culture.
Probably because of the simplicity of its definition, the concept of π has become entrenched in popular culture to a degree far greater than almost any other mathematical construct.[2] It is, perhaps, the most common ground between mathematicians and non-mathematicians.[3] Reports on the latest, most-precise calculation of π (and related stunts) are common news items.[4][5][6] The current record for the decimal expansion of π, if verified, stands at 5 trillion digits.[7]
The Greek letter π, often spelled out pi in text, was first adopted for the number as an abbreviation of the Greek word for perimeter "περίμετρος" (or as an abbreviation for "perimeter/diameter") by William Jones in 1707. The constant is also known as Archimedes' Constant, after Archimedes of Syracuse, although this name is uncommon in modern English-speaking contexts.
-
ccc rammstein ccc günaydın diler 30 12 2024
-
 sözlük bitmiş beyler la
sözlük bitmiş beyler la -
 gay pataklayan eğer delikanliysan yarın
gay pataklayan eğer delikanliysan yarın -
 bıcakklamak istedigim yazarr
bıcakklamak istedigim yazarr -
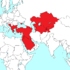 2080 türkiye nüfusu
2080 türkiye nüfusu -
 kirazdankupe selam naber surtk
kirazdankupe selam naber surtk -
 panter emel gel lan burayaa
panter emel gel lan burayaa -
 eksi sözlükk kızlarıı
eksi sözlükk kızlarıı -
elim titreye titreye kombinin
-
 beyler endonezyalı bir kıza yürümeyi
beyler endonezyalı bir kıza yürümeyi -
 kamyoncukamil anladın sen
kamyoncukamil anladın sen -
 telefon benim aletten uzun
telefon benim aletten uzun -
iyi geceler gaziemirde hava 6 derece
-
izmirli laik bir adamım
-
 kendimjse nasil engeli raporu cikartabiliris
kendimjse nasil engeli raporu cikartabiliris -
yarın akşam silahlı saldırı adam yaralama ve gasp
-
 gwynplaine kalemini kırdım
gwynplaine kalemini kırdım -
saglik kadar degerli bise yok
-
boyum 10 cm kisalsaydi
-
çetgpt den inci sözlük fıkrası
-
kiz olsaydim şu an tiktokta hediye
-
 gözümde the vikings nasıl mı işte böyle
gözümde the vikings nasıl mı işte böyle -
flörttür sohbettir falan bunlar hep beta erkek işi
-
kedi köpek bile sigisyor
-
karı yarı çıplak geziyor
-
türkiyeliyim diyen vatansevere kin kusan kitle
-
 bu sabah 6 sularında klagib arabaya binen
bu sabah 6 sularında klagib arabaya binen -
bir kürt bir gün vergi dairesine girmiş
-
ulan gunduz oynanan portekiz ligi maclari
-
beyler türküm ama kendimi ermeni gibi
- / 2