Başlık biraz gecikti, yoğun olduğumdan dolayı açamadım.

(Merakı olmayan burada okumayı bıraksın, sonra "çok uzun, kör oldum, kafam gibildi" vs. demeyin.)

Birçoğunuzun bildiği gibi dolaşık parçacıklar, birinin belirli bir durumdaki davranışını -örneğin +z yönündeki açısal momentum- ölçtüğümüzde, diğerinin de davranışını tahmin edebildiğimiz çifterdir.

Peki nasıl olabiliyor böyle bir şey?

Klagib mekanikten bildiğimiz simetri ve korunum yasaları -tam olarak olmasa da- kuantum mekaniğinde de geçerlidir. Olay da özünde buna dayanır.

Bunu anlar gibi olmanın en basit yolu, bir fotondan oluşan elektron-pozitron çiftini (görsel) ele almaktır. Bu çift oluştuğunda spinleri belirli bir eksene göre ya antiparalel (birbirine zıt), ya da paralel olmaktadır. Paralel ya da antiparalel durum, bu ikili sistem için daima korunmalıdır (klagib açısal momentum korunumuna benzetilebilir, ama sadece benzetin, aslında oldukça farklı), mesafe ne olursa olsun.

Bunun sonuçları oldukça ilginçtir. Şöyle ki, bir gözlemcinin yaptığı ölçüm, aralarındaki uzaklık ne olursa olsun, başka bir gözlemcinin yaptığı ölçümün sonucunu etkileyebilir.

To be continued...

edit: Anlatacaklarım bu kadar. Genelde bu tarz konuları, bu şekilde sözel ağırlıklı anlatmayı sevmem. Bir hatam olduysa veya yanlış anlaşılmalara sebep olduysam şimdiden özür dilerim.

Tahmin etmiş olabileceğiniz gibi, Bell\'in yapmak istediğiyle yaptığı tamamen farklıydı.

Teoremiyle; dolanıklık gibi kuantum fenomenlerinin, yerellik ilkesi dahilinde, herhangi bir klagib gizli değişken teorisi ile açıklanamayacağını gösterdi.

Nasıl mı? Alın size paralel spinler için basit bir Bell eşitsizliği:


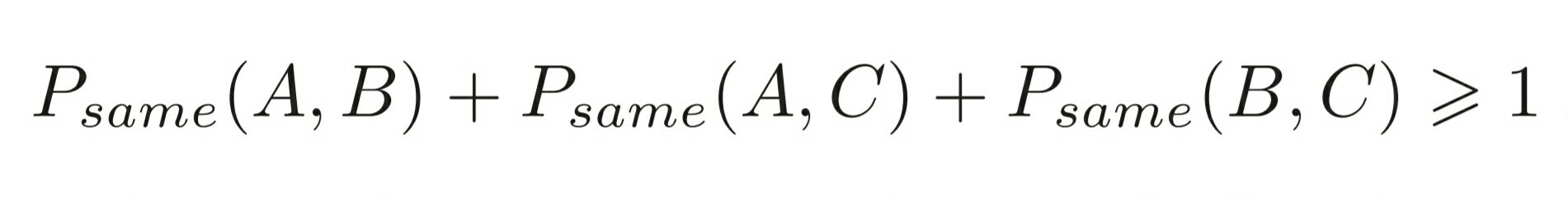
A, B ve C farklı açılara ayarlanmış ölçüm cihazları, P(A, B) ise A ve B cihazlarının aynı sonucu verme olasılığı (ikisinin de |u> ya da |d> olması).

Ha bir de şunu sağlamalı:

P(A, A) = P(B, B) = P(C, C) = 1

Sonuçta dolaşık parçacıklardan bahsediyoruz. Aynı eksenlerde paralel spinlere -zıt spinler için de olabilirdi- sahip olmalılar.

Velhasılıkelam, gizli değişken teorileri bu eşitsizliğe uymalıdır. Çünkü bu değişkenlerin sonucunda, ölçüm cihazları için önceden belirlenmiş, belirli sayıda (A, B, C) kombinasyonu olmalıdır.

Oysa kuantum mekaniğinin öngörüleri bu eşitsizlikle uyumlu değildir. Çünkü ortada önceden belirlenen bir şey yoktur. Daha önce de dediğim gibi, kuantum mekaniğinde olasılık genlikleri vardır. Bu genlikler de ölçüm ekseninin farklı açıları için dönme matrislerinin terimleridir.

Örneğin y ekseni etrafında θ'lık dönme için; +x yönünde spine sahip yarım spinli bir parçacığın, ölçümden sonra +x' yönünde spine sahip olma genliği cos(θ/2), olasılığı cos²(θ/2)'dir.

Bunu da wiki'de buldum, aradaki uyumsuzluğun basit bir gösterimi:


1 ile 0 u ve d'ye karşılık geliyor. Ψ ise özel bir genlikler kümesi, gerisi hesap kitap zaten.

Öncelikle, geçen bölümdeki 2. öncülün neden doğru olmadığıyla başlayalım.

Kuantum mekaniğinde; bir parçacıkla ilgili ölçüm yaptığınız zaman, parçacığın durumunu belirli bir değere "çökertirsiniz." Örneğin en basitinden (üzgünüm, notasyon kullanmam gerek):

1/√2(|u> + |d>)

(u spin yukarı, d spin aşağı durumu temsil ediyor. 1/√2 ise bu durumların genliği, bu genliğin karesi yani 1/2 ise her bir durumun olasılığını veriyor.)

Durumundaki bir parçacık üzerinde ölçüm yaparsanız, |u> veya |d> durumunun bir değerini elde edersiniz, artık parçacık iki durumdan birindedir.

(x ve y ekseninde belirli spin değerlerine sahip bir parçacığın durumu, "dönme matrisleri" vasıtası ile yukarıdaki durumun farklı varyasyonları şeklinde yazılabilir, daha sonra buraya döneceğiz.)

Kısaca, B'deki gözlemci ölçüm yaptığı anda, A'daki gözlemcinin yaptığı ölçüm yalan olur. Tabii ki tam tersi de geçerli.

Gizli Değişkenler ve Bell Eşitsizlikleri

"EPR ne önermiş?" diyorduk. Özetle; parçacıkların, tüm ölçüm kombinasyonları için, spinleri aynı eksenlerde paralel veya antiparalel olacak şekilde, bazı bilinmeyen değişkenlere göre davrandıklarını öne sürdüler.

Bu yaklaşıma göre herhangi bir bilgi aktarımına gerek yoktu, çünkü gerekli bilgiye zaten parçacıklar sahipti.

ismi "gizli değişkenler", çünkü bu bilgilerin nerede, nasıl kodlandığını bilmiyoruz, bu da kuantum kurdıbının tam bir kuram olmadığı anldıbına geliyor(du). Einstein ve destekçilerine göre tabii.

E haliyle bir EPR destekçisi olan John Stewart Bell amcamız da, gizli değişkenlerin var olduğunu ispatlamak istemiş.

işler istediği gibi gitmemiş tabii...

EPR (Einstein-Podolsky-Rosen) Paradoksu

Tahmin edilebileceği üzere, başta Einstein olmak üzere bazı fizikçiler, geçen bölümdeki son cümleye karşı çıktı ve bir kağıt yayımladı. Onlara göre kısaca:

1- Bu durum yerellik ilkesine uymaz, çünkü bilginin ışıktan hızlı aktarılmasını gerektirir, bu da beraberinde çelişkiler doğrudur.

2- Bu, aynı zamanda Heisenberg'in belirsizlik ilkesine aykırıdır, şu şekilde:

A ve B konumlarında, dolaşık bir çift için gözlem yapan iki gözlemci varsayalım.

A gözlemcisi, parçacıklardan birinin x eksenindeki spinini ölçerken, B gözlemcisi de y eksenindeki spinini ölçsün. A gözlemcisi x ekseni için aldığı sonuçtan hareketle, diğer parçacığın bu eksen için ölçüm sonucunu tahmin edebilir ve bunu B'ye aktarabilir. Böylelikle B gözlemcisi, kendi parçacığının hem y eksenindeki, hem de x eksenindeki iç açısal momentumunu öğrenmiş olur.

Peki bu sözde çelişkilerin üzerine, Einstein ve saz arkadaşları, birbiriyle uyumlu hareket eden dolaşık çiftleri nasıl açıkladı? Ve bu ünlü kağıdın problemi neydi?

Gizli değişkenler, Bell eşitsizliği ve daha fazlası ile devam edecek...

feynman'ın kayıp dölü

zevkle okudum, eline sağlık. ama satır aralarında birkaç bakınız bırakmak şart gibi. konu bütünlüğünü daha iyi kavramak açısından;

(bkz: yerellik ilkesi)
(bkz: kopenhag yorumu)
(bkz: schrödingerin kedisi) kopenhag yorumuna bağlı olarak gözlemci bilincinin önemini çok temiz açıklıyor.

bir de;
(bkz: aspect deneyi)

ilgilisine güzel bir başlık. Teşekkürler.

uygulamadan giriyorum cevaplama konusunda sıkıntı çıkarıyor, şu sicim teorisi hakkındaki entryne buradan cevap yazayım dedim.
bu teori, eğer bir şekilde tamamlanabilirse yaradılışın tümünün mantığını açıklayabileceğini iddia eden ve hatta "her şeyin teorisi" diye de anılan, belki de günümüzdeki EN iddialı teori olduğu için çok fazla sorumun doğmasına sebep oluyor. teoriyle ilgili her kaynakta farklı bir şey yazıyor ve herkes başka bir şey iddia ediyor. ortada böylesine büyük bir iddia olmasına rağmen fikirlerin böylesine açık uçlu olması gerçekten beynimi bulandırıyor ara ara. tatmin edici cevabın için teşekkür ederim.

(bkz: sözlük arşivim) eklerim panpa

Eline sağlık panpa

Şey cok sacma
Newton fiziginde (basit fizik) enerji hiç yok olmuyor hep korunuyordu
Modern fizikte(kuantum)
Parçaciklar carpisinca enerjin8m bir kisminin yok olmasi çok saçma degil mi

R.e.z= N

Seviye yükselt hoca

Rezeets

Okuyacağım panpa

Bı ihtimal

Rezervasyon

bir soru: şayet ilerleyen yıllarda "sicim teorisi" tamamlanıp bir kurala dönüştürülebilirse, insanoğlunun "gerçeklik" kavramı hakkındaki sorularının tümü cevaplarını bulabilecek mi? bu konu hakkındaki görüşünü merak ediyorum.

Okurum.

iyimiş lan