Tahmin etmiş olabileceğiniz gibi, Bell\'in yapmak istediğiyle yaptığı tamamen farklıydı.

Teoremiyle; dolanıklık gibi kuantum fenomenlerinin, yerellik ilkesi dahilinde, herhangi bir klagib gizli değişken teorisi ile açıklanamayacağını gösterdi.

Nasıl mı? Alın size paralel spinler için basit bir Bell eşitsizliği:


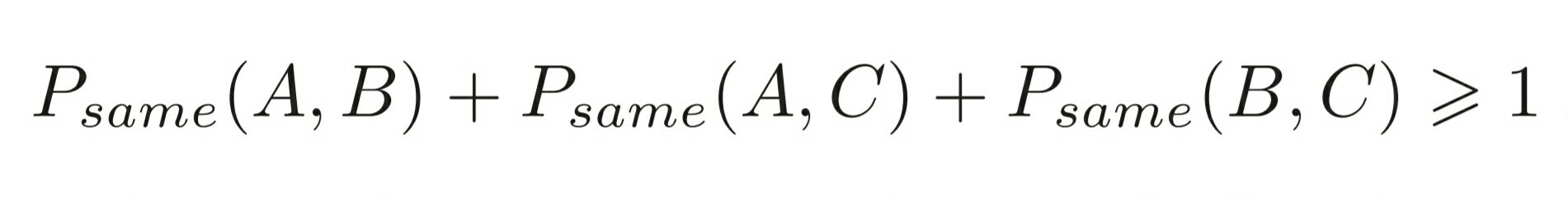
A, B ve C farklı açılara ayarlanmış ölçüm cihazları, P(A, B) ise A ve B cihazlarının aynı sonucu verme olasılığı (ikisinin de |u> ya da |d> olması).

Ha bir de şunu sağlamalı:

P(A, A) = P(B, B) = P(C, C) = 1

Sonuçta dolaşık parçacıklardan bahsediyoruz. Aynı eksenlerde paralel spinlere -zıt spinler için de olabilirdi- sahip olmalılar.

Velhasılıkelam, gizli değişken teorileri bu eşitsizliğe uymalıdır. Çünkü bu değişkenlerin sonucunda, ölçüm cihazları için önceden belirlenmiş, belirli sayıda (A, B, C) kombinasyonu olmalıdır.

Oysa kuantum mekaniğinin öngörüleri bu eşitsizlikle uyumlu değildir. Çünkü ortada önceden belirlenen bir şey yoktur. Daha önce de dediğim gibi, kuantum mekaniğinde olasılık genlikleri vardır. Bu genlikler de ölçüm ekseninin farklı açıları için dönme matrislerinin terimleridir.

Örneğin y ekseni etrafında θ'lık dönme için; +x yönünde spine sahip yarım spinli bir parçacığın, ölçümden sonra +x' yönünde spine sahip olma genliği cos(θ/2), olasılığı cos²(θ/2)'dir.

Bunu da wiki'de buldum, aradaki uyumsuzluğun basit bir gösterimi:


1 ile 0 u ve d'ye karşılık geliyor. Ψ ise özel bir genlikler kümesi, gerisi hesap kitap zaten.